The GAUSS_QUAD_LEGENDRE function returns an array containing the x values (the abscissas) for Gaussian quadrature integration, where the x values are the roots of the Legendre polynomial of order N. The routine also returns the weighting coefficients as an output keyword.
Given a function f(x), the Gaussian integration formula for the Gauss-Legendre case can be written as:
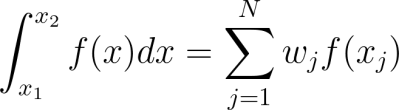
where wj are the integration weights, computed using the following formula:
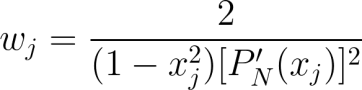
and PN is the Legendre polynomial of order N.
GAUSS_QUAD_LEGENDRE returns xj in the result, and wj in the WEIGHTS keyword.
GAUSS_QUAD_LEGENDRE is based on the routine gauleg described in section 4.5 of Numerical Recipes in C: The Art of Scientific Computing (Second Edition), published by Cambridge University Press, and is used by permission.
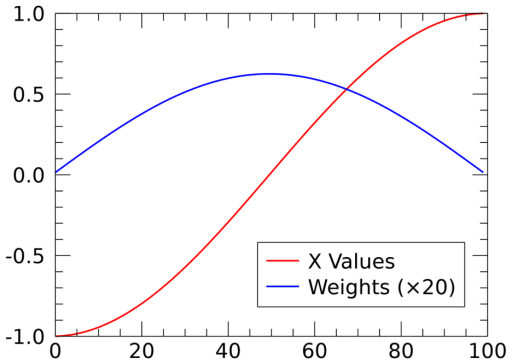
Examples
Compute the x locations and weights for N=100:
x = gauss_quad_legendre(-1, 1, 100, weights=w)
p1 = plot(x, 'r2', font_size=18, name='X Values')
p2 = plot(w * 20, 'b2', /overplot, name='Weights ($\times$20)')
l = legend(target=[p1, p2], position=[0.88, 0.35], font_size=18)
Syntax
Result = GAUSS_QUAD_LEGENDRE( Lower, Upper, Order, EPS=value, WEIGHTS=variable )
Return Value
The result is a double-precision array containing the x locations (the abscissas) for the Gauss-Legendre quadrature integration formula.
Arguments
Lower
A number giving the lower limit of integration.
Upper
A number giving the upper limit of integration.
Order
A positive integer giving the order of the Legendre polynomial.
Keywords
EPS
Set this keyword to the desired precision of the results. The default is 1d-12.
WEIGHTS
Set this keyword to a named variable in which to return the integration weights.
Version History
See Also
SPHERE_HARM_FORWARD