The SPHERE_HARM_FILTER function uses the spherical harmonic transform to perform a spectral filter on a two-dimensional array of data values on a sphere.

The filter kernel is based on the isotropic smoothing function of Sardeshmukh and Hoskins (Monthly Weather Review, 1984). The filter has the following form:

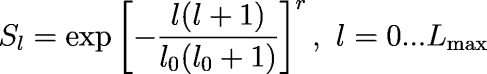
where l0 is the truncation parameter and r is the exponent.

For details on the spherical harmonic transform see SPHERE_HARM_FORWARD.

SPHERE_HARM_FILTER is based on the original filtersh routine written by Gilbert P. Compo, and is used with permission.

SPHERE_HARM_FILTER was converted from the original filtersh routine written by Gilbert P. Compo, and is used with permission. The algorithm is based upon the following paper:

Sardeshmukh, P. D., and B. I. Hoskins, 1984: Spatial Smoothing on the Sphere. Mon. Wea. Rev., 112, 2524–2529, https://doi.org/10.1175/1520-0493(1984)112<2524:SSOTS>2.0.CO;2.

This routine is written in the IDL language. Its source code can be found in the file sphere_harm_filter.pro in the lib subdirectory of the IDL distribution.

Example

In this example, we compute the T63 truncation on a two-dimensional array of air temperatures from 1 Dec 1884:

restore, filepath('reanl20v3_1dec1884_512x256dbl.sav', subdir=['examples', 'data'])
T63 = sphere_harm_filter(A, 63)
print, stdev(A), stdev(T63)

IDL prints:

  18.781273       18.642773

For a more detailed example as well as data credits and reference, see SPHERE_HARM_FORWARD.

Syntax

Result = SPHERE_HARM_FILTER( Array, Truncate, RVAL=value )

Return Value

The result is a double-precision vector of length Lmax + 1.

Arguments

Array

An input array of real values, A(φ, θ) of dimensions [nphi, ntheta], where nphi is the number of longitude points and ntheta is the number of latitude points. The array must have dimensions nphi = 2 * ntheta.

Truncate

An integer giving the total spectral wavenumber at which the filter has e–1 power. This corresponds to l0 in the equation above.

Keywords

RVAL

Set this keyword to the exponent of the smoothing function. This corresponds to r in the equation above. Possible values are:

  • RVAL = 1 corresponding to del2 diffusion

  • RVAL = 2 corresponding to del4 diffusion

  • RVAL = 3 corresponding to del6 diffusion

A higher exponent will give a sharper cutoff, but will introduce more Gibbs ringing. The default is 1.

Version History

9.1

Introduced

See Also

SPHERE_HARM_FORWARD, SPHERE_HARM_INVERSE, SPHERE_HARM_KERNEL