The SPHERE_HARM_KERNEL function constructs the kernel coefficients for a triangular filter of a spherical harmonic transform using the isotropic smoothing function of Sardeshmukh and Hoskins (Monthly Weather Review, 1984).
The filter has the following form:
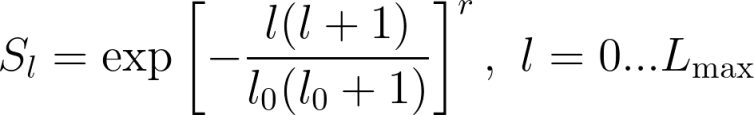
where l0 is the truncation parameter and r is the exponent.
The SPHERE_HARM_KERNEL function is typically called automatically by SPHERE_HARM_FILTER, but is provided as a standalone function in case you want to examine the coefficients or perform the filter manually.
For details on the spherical harmonic transform see SPHERE_HARM_FORWARD.
SPHERE_HARM_KERNEL is based on the original filtersh routine written by Gilbert P. Compo, and is used with permission.
This routine is written in the IDL language. Its source code can be found in the file sphere_harm_kernel.pro in the lib subdirectory of the IDL distribution.
Example
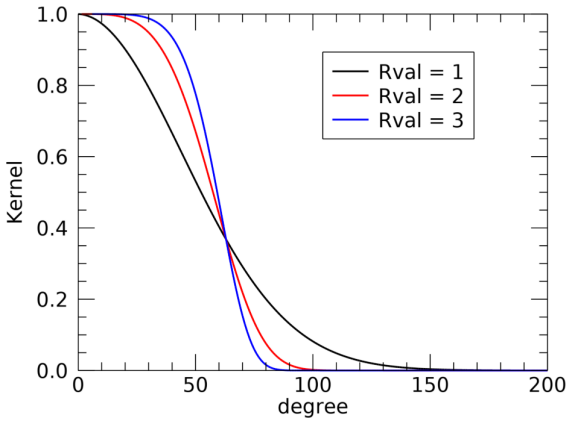
In this example, we compute the T63 truncation with Lmax=256:
s1 = sphere_harm_kernel(256, 63)
p1 = plot(s1, '2', xrange = [0, 200], name = 'Rval = 1', $
xtitle='degree', ytitle='Kernel', font_size = 16)
s2 = sphere_harm_kernel(256, 63, rval = 2)
p2 = plot(s2, '2r', /overplot, name = 'Rval = 2')
s3 = sphere_harm_kernel(256, 63, rval = 3)
p3 = plot(s3, '2b', /overplot, name = 'Rval = 3')
l = legend(target = [p1, p2, p3], $
position = [0.8, 0.8], font_size = 16)
Syntax
Result = SPHERE_HARM_KERNEL( Lmax, Truncate, RVAL=value )
Return Value
The result is a double-precision vector of length Lmax + 1.
Arguments
Lmax
An integer giving the maximum degree l that was used for the spherical harmonic transform.
Truncate
An integer giving the total spectral wavenumber at which the filter has e–1 power. This corresponds to l0 in the equation above.
Keywords
RVAL
Set this keyword to the exponent of the smoothing function. This corresponds to r in the equation above. Possible values are:
-
RVAL = 1 corresponding to del2 diffusion
-
RVAL = 2 corresponding to del4 diffusion
-
RVAL = 3 corresponding to del6 diffusion
A higher exponent will give a sharper cutoff, but will introduce more Gibbs ringing. The default is 1.
Version History
See Also
SPHERE_HARM_FORWARD, SPHERE_HARM_INVERSE, SPHERE_HARM_FILTER