The QROMB function evaluates the integral of a function over the closed interval [A, B] using Romberg integration.

Examples

For more information on using QROMB, see Additional Examples.

Example 1

To integrate the CUBIC function (listed above) over the interval [0, 3] and print the result:

PRINT, QROMB('cubic', 0.0, 3.0)

IDL prints:

 32.2500

This is the exact solution.

Syntax

Result = QROMB( Func, A, B [, /DOUBLE] [, EPS=value] [, JMAX=value] [, K=value] )

Return Value

The result will have the same structure as the smaller of A and B, and the resulting type will be single- or double-precision floating, depending on the input types.

Arguments

Func

A scalar string specifying the name of a user-supplied IDL function to be integrated. This function must accept a single scalar argument X and return a scalar result. It must be defined over the closed interval [A, B].

For example, if we wish to integrate the cubic polynomial

y = x3 + (x - 1)2 + 3

we define a function CUBIC to express this relationship in the IDL language:

FUNCTION cubic, X
   RETURN, X^3 + (X - 1.0)^2 + 3.0
END

Note: If QROMB is complex then only the real part is used for the computation.

A

The lower limit of the integration. A can be either a scalar or an array.

B

The upper limit of the integration. B can be either a scalar or an array.

Note: If arrays are specified for A and B, then QROMB integrates the user-supplied function over the interval [Ai, Bi] for each i. If either A or B is a scalar and the other an array, the scalar is paired with each array element in turn.

Keywords

DOUBLE

Set this keyword to force the computation to be done in double-precision arithmetic.

EPS

The desired fractional accuracy. For single-precision calculations, the default value is 1.0 x 10-6. For double-precision calculations, the default value is 1.0 x 10-12.

JMAX

2(JMAX - 1) is the maximum allowed number of steps. If this keyword is not specified, a default of 20 is used.

K

Integration is performed by Romberg’s method of order 2K. If not specified, the default is K=5. (K=2 is Simpson’s rule).

Additional Examples

Example 2

This example evaluates the volume under a surface using the following double integration:

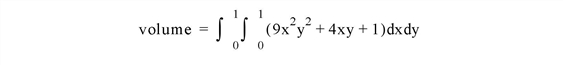
The exact solution to this equation is 3.

The example consists of four routines: the main routine, the integration in the y direction, the second integration of the x coefficient, and the second integration of the x2 coefficient. The main routine is the last routine in the program. To run this example, copy the text of all four routines, paste them into an IDL editor window, and save the window’s contents as DoubleIntegration.pro.

FUNCTION XSquaredCoef, x
 
   ; Integration of the x squared coefficient.
   secondIntegration = 9.*x^2
   RETURN, secondIntegration
 
END
 
FUNCTION XCoef, x
 
   ; Integration of the linear x coefficient.
   secondIntegration = x
   RETURN, secondIntegration
 
END
 
FUNCTION YDirection, y
 
   ; Re-write equation to consider both x coefficents.
   firstIntegration = QROMB('XSquaredCoef', 0., 1.)*y^2 $
   + 4.*(QROMB('XCoef', 0., 1.))*y + 1.
   RETURN, firstIntegration
 
END
 
PRO DoubleIntegration
 
   ; Determine the volume under the surface represented
   ; by 9x^2y^2 + 4xy + 1 over a specific region.
   volume = QROMB('YDirection', 0., 1. )
 
   ; Output results.
   PRINT, 'Resulting Volume:  ', volume
 
END

Example 3

This example evaluates the mass of a volume using the following triple integration on a three-dimensional equation representing its density:

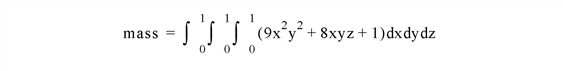
The exact solution to this equation is 3.

The example consists of six routines: the main routine, the integration in the z-direction, the second integration of the xy coefficient, the second integration of the second x2y2 coefficient, the third integration in the x coefficient, and the third integration in the x2 coefficient. The main routine is the last routine in the program. To run this example, copy the text of all six routines, paste them into an IDL editor window, and save the window’s contents as TripleIntegration.pro.

FUNCTION XSquaredCoef, x
 
   ; Integration of the x squared coefficient.
   thirdIntegration = 9.*x^2
   RETURN, thirdIntegration
 
END
 
FUNCTION XCoef, x
 
   ; Integration of the linear x coefficient.
   thirdIntegration = x
   RETURN, thirdIntegration
 
END
 
FUNCTION XSquaredYSquaredCoef, y
 
   ; Integration of the y squared coefficient.
   secondIntegration = QROMB('XSquaredCoef', 0., 1.)*y^2
   RETURN, secondIntegration
 
END
 
FUNCTION XYCoef, y
 
   ; Integration of the linear y coefficient.
   secondIntegration = QROMB('XCoef', 0., 1.)*y
   RETURN, secondIntegration
 
END
 
FUNCTION ZDirection, z
 
   ; Re-write equation to consider all the x and y
   ; coefficients.
   firstIntegration = QROMB('XSquaredYSquaredCoef', 0., 1.) + $
   8.*(QROMB('XYCoef', 0., 1.))*z + 1.
   RETURN, firstIntegration
 
END
 
PRO TripleIntegration
 
   ; Determine the mass of the density represented
   ; by 9x^2y^2 + 8xyz + 1 over a specific region.
   mass = QROMB('ZDirection', 0., 1. )
 
   ; Output results.
   PRINT, 'Resulting Mass:  ', mass
 
END

Version History

4.0

Introduced

Resources and References

QROMB is based on the routine qromb described in section 4.3 of Numerical Recipes in C: The Art of Scientific Computing (Second Edition), published by Cambridge University Press, and is used by permission.

See Also

INT_2D, INT_3D, INT_TABULATED, QROMO, QSIMP