The IMSL_BOXCOXTRANS function performs a forward or an inverse Box-Cox (power) transformation.
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
The IMSL_BOXCOXTRANS function performs a forward or an inverse Box-Cox
(power) transformation of n = N_ELEMENTS(z) observations {Zt} for t = 0, 1, ..., n–
1.
The forward transformation is useful in the analysis of linear models or models with non-normal errors or non-constant variance (Draper and Smith 1981, p. 222). In the time series setting, application of the appropriate transformation and subsequent differencing of a series can enable model identification and parameter estimation in the class of homogeneous stationary autoregressive-moving average models. The inverse transformation can later be applied to certain results of the analysis, such as forecasts and prediction limits of forecasts, in order to express the results in the scale of the original data. A brief note concerning the choice of transformations in the time series models is given in Box and Jenkins (1976, p. 328).
The class of power transformations discussed by Box and Cox (1964) is defined by:
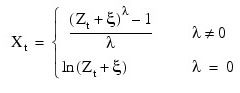
where Zt + ξ > 0 for all t. Since:
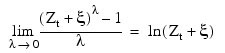
the family of power transformations is continuous.
Let λ = power and ξ = S; then, the computational formula used by IMSL_BOXCOXTRANS is given by:
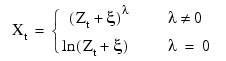
where Zt + ξ > 0 for all t. The computational and Box-Cox formulas differ only in the scale and origin of the transformed data. Consequently, the general analysis of the data is unaffected (Draper and Smith 1981, p. 225).
The inverse transformation is computed by:
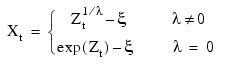
where {Zt} now represents the result computed by IMSL_BOXCOXTRANS for a forward transformation of the original data using parameters λ and ξ.
Examples
Example 1
The following example performs a Box-Cox transformation with power = 2.0 on 10 data points.
power = 2.0
z = [1.0, 2.0, 3.0, 4.0, 5.0, 5.5, 6.5, 7.5, 8.0, 10.0]
x = IMSL_BOXCOXTRANS(z, power)
PM, x, Title = 'Transformed
IDL prints:
Data'Transformed Data
1.00000
4.00000
9.00000
16.0000
25.0000
30.2500
42.2500
56.2500
64.0000
100.000
Example 2
This example extends the first example; an inverse transformation is applied to the transformed data to return to the original data values.
power = 2.0
z = [1.0, 2.0, 3.0, 4.0, 5.0, 5.5, 6.5, 7.5, 8.0, 10.0]
x = IMSL_BOXCOXTRANS(z, power)
PM, x, Title = 'Transformed Data'
Transformed Data
1.00000
4.00000
9.00000
16.0000
25.0000
30.2500
42.2500
56.2500
64.0000
100.000
y = IMSL_BOXCOXTRANS(x, power, /inverse)
PM, y, Title = 'Inverse Transformed Data'
IDL prints:
Inverse Transformed Data
1.00000
2.00000
3.00000
4.00000
5.00000
5.50000
6.50000
7.50000
8.00000
10.0000
Errors
Fatal Errors
STAT_ILLEGAL_SHIFT: S = # and the smallest element of z is z(#) = #. S plus z(#) = #. S + z(I) must be greater than 0 for i = 1, ..., N_ELEMENTS(z). N_ELEMENTS(z) = #.
STAT_BCTR_CONTAINS_NAN: One or more elements of z is equal to NaN (Not a number). No missing values are allowed. The smallest index of an element of z that is equal to NaN is #.
STAT_BCTR_F_UNDERFLOW: Forward transform. power = #. S = #. The minimum element of z is z(#) = #. (z(#)+ S) ^ power will underflow.
STAT_BCTR_F_OVERFLOW: Forward transformation. power = #. S = #. The maximum element of z is z(#) = #. (z(#) + S) ^ power will overflow.
STAT_BCTR_I_UNDERFLOW: Inverse transformation. power = #. The minimum element of z is z(#) = #. exp(z(#)) will underflow.
STAT_BCTR_I_OVERFLOW: Inverse transformation. power = #. The maximum element of z(#) = #. exp(z(#)) will overflow.
STAT_BCTR_I_ABS_UNDERFLOW: Inverse transformation. power = #. The element of z with the smallest absolute value is z(#) = #. z(#) ^ (1/power) will underflow.
STAT_BCTR_I_ABS_OVERFLOW: Inverse transformation. power = #. The element of z with the largest absolute value is z(#) = #. z(#) ^ (1/ power) will overflow.
Syntax
Result = IMSL_BOXCOXTRANS(Z, Power [, /DOUBLE] [, /INVERSE] [, S=parameter])
Return Value
One-dimensional array containing the transformed data..
Arguments
Power
Exponent parameter in the Box-Cox (power) transformation.
Z
One-dimensional array containing the observations.
Keywords
DOUBLE (optional)
If present and nonzero, double precision is used.
INVERSE (optional)
If present and nonzero, the inverse transform is performed.
S (optional)
Shift parameter in the Box-Cox (power) transformation. Parameter shift must satisfy the relation min (z(i)) + S > 0. Default: 0.0.
Version History