The IMSL_TIE_STATS function computes tie statistics for a sample of observations.
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
The IMSL_TIE_STATS function computes tie statistics for a monotonically increasing sample of observations. Tie statistics are statistics that may be used to correct a continuous distribution theory nonparametric test for tied observations in the data. Observations i and j are tied if the successive differences x(k + 1) – x(k), inclusive, are all less than FUZZ. Note that if each of the monotonically increasing observations is equal to its predecessor plus a constant, if that constant is less than FUZZ, then all observations are contained in one tie group. For example, if FUZZ = 0.11, then the following observations are all in one tie group.
Example
This example will compute tie statistics for a sample of length 7.
fuzz = 0.001
x = [1.0, 1.0001, 1.0002, 2.0, 3.0, 3.0, 4.0]
tstat = IMSL_TIE_STATS(x, FUZZ = fuzz) PRINT, tstat
4.00000 2.50000 84.0000 6.00000
Syntax
Result = IMSL_TIE_STATS(X [, /DOUBLE] [, FUZZ=value])
Return Value
One-dimensional array of length 4 containing the tie statistics.
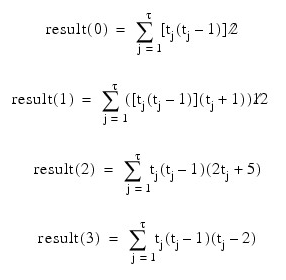
where tj is the number of ties in the j-th group (rank) of ties, and τ is the number of tie groups in the sample.
Arguments
X
One-dimensional array containing the observations. X must be ordered monotonically increasing with all missing values removed.
Keywords
DOUBLE (optional)
If present and nonzero, double precision is used.
FUZZ (optional)
Nonnegative constant used to determine ties. Observations i and j are tied if the successive differences x(k + 1) – x(k) between observations i and j, inclusive, are all less than FUZZ. Default: 0.0
Version History